
-----
Crowsfoot with torque wrench. What's the math? p.2
< Prev. page (You're on the last page of the thread)
Q. In thinking about this question, isn't the length of the torque wrench really not related? (I see that the calculators factor it in & everyone seems to include it in their calculations). Torque is a force over distance (usually lbs/inch or lbs/feet), which already has the distance component included. I'm thinking that if you had two torque wrenches, a 6" long torque wrench, and a 12" long torque wrench, and used them both to tighten bolts to 25 lbs/ft, the bolts are going to all be tightened the same. Yes, you have to pull harder on the 6" wrench than the 12" wrench, but the net resultant torque is the same if you tighten everything to 25 lbs/ft on the dial. Now if you put the same crows foot wrench on each torque wrench and make the calculated adjustment for each wrench (which factors in the wrench length) you will end up with a different indicated value to tighten to for each wrench. This doesn't seem right. What am I missing here?
Ned Lloyd- North East, Connecticut
September 9, 2008
A. When we use an extension on a torque wrench, the torque wrench does not know the extension exists and therefore, cannot account for the extension. If your torque setting is 500 ft-lbs and the extension is as long as the torque wrench, the torque wrench will still think you are tightening to 500 ft-lbs. Meaning the resultant torque at the point where the torque wrench and extension are adjoined is 500 ft-lbs. But, since the extension is as long as the torque wrench, the resultant torque applied at the bolt is doubled or 1,000 ft-lbs.
But, what happens now when you use a multiplier that is say 6:1 and the extension? At first, you would think that the resultant torque at the bolt would be 6,000 ft-lbs. But, with this multiplier, the extension and the multiplier are always colinear. The torque wrench and multiplier are not. The torque wrench makes six revolutions for every one revolution of the multiplier and extension. We are tightening a B-lock and need to tighten the bolt such that the multiplier makes 90 degree increments. In order for this to happen, the torque wrench must rotate 540 degrees. When the torque wrench rotates 90°, it is at a 75° [90°-(90°/6)] angle with the extension. When the torque wrench rotates 180°, it is at a 150° angle with the extension. 270°-->225°, 360°-->300°, 450°-->375°, and finally when the torque wrench rotates 540°, it is at a 375° angle with the extension. So, if the torque setting on the torque wrench is 500 ft-lbs, the extension is as long as the torque wrench, and you are using a 6:1 multiplier, is the resultant torque on the bolt always 6,000 ft-lbs? Or does it change with the angle between the wrench and extension?
OEM - Saginaw, Michigan
This was an interesting thread which answered my search for crows foot extension calculations. However several posts refer to the use of a long extension bars along the axis of the bolt and question if this has an effect. When using a long bar it is necessary to apply an equal and opposite force to the direction you pull on the wrench. When using the socket directly, the bolt or stud provides this force but with the long extension the socket acts as a joint and allows the bar to lean. Providing you keep the extension bar in line with the bolt axis the torque will be correct. If you allow the extension to lean towards the wrench you effectively extend the distance of the wrench from the bolt axis and this will increase the torque applied to the bolt or nut in the same way a crows foot extension does. For small misalignment angles this change will not make much difference but if a number of extensions are fixed together the offset from the bolt axis becomes significant and causes increase torque to be applied to the fixing. Unlike the crows foot this is difficult to calculate as the misalignment will vary.
Nick Carton- Birmingham,West Midlands,UK
A. Richard is correct. The formula used to calculate a crowsfoot attachment mounted at 0 degrees is...
M1 = M2 x L1 / L2
M1 is the torque setting of the wrench.
M2 is the actual torque applied to the nut
L1 is the normal length of the wrench
L2 is the extended length of the wrench (Length of wrench + length of adapter)
Attaching the crowsfoot at 90 degrees on the torque wrench will not change the torque value enough to matter.
Using a "solid" extension will not change the torque value enough to matter. (Torque is still being applied in the same axial plane.)
Remember... Torque = Force x Radius
wind turbine technician - Clear Lake, South Dakota
A. I prefer a simpler formula:
Wrench Torque = Required Torque / (1 + Extension Length)
Where Extension Length is the distance between wrench drive rotating axis to the fastener rotating axis on the crowsfoot.
For example, to determine the torque to set on the wrench when a torque of 50 Nm is required on the fastener while a crowsfoot with extension length of 40 mm is used:
Wrench Torque = 50 Nm / (1 + 0.04 m)
Wrench Torque = 48.0769 Nm
- Dublin, Ireland
Thanks all for this informative thread! I am submitting what I believe is the reason why people write that 90-degree extensions have no appreciable effect on torque applied vs. torque setting:
If you have a 14" wrench and use a 2" extension at 90 degrees to the wrench (in my case so the wrench will clear the tire when I torque the lug nuts), the length of the lever is 14.14", a 1% difference and within the 3% error range of most torque wrenches in this size.
The wrench and the extension form two legs of a right triangle, and the (imaginary) hypotenuse is the effective length of the lever applying torque at the nut. Using the Pythagorean Theorem,
c = sqrt(14^2 + 2^2) = sqrt(200) = 14.14
I also wanted to report a broken link. One writer (May -, 2007) referred to a calculator, which has moved on the target website. A new link to all 3 of their calculators is:
www.norbar.com/Calculators/tabid/57/Default.aspx
Chris Niggeler- Edgewood, New Mexico
February 9, 2009
Google "torque offset calculator". it will point to cncexpo which has several useful pages of different information.
Miles Thompson- Selma, Alabama
Thanks, Miles. But the thread started with David's complaint that he was googling and following links and not learning much from all the time -- so could you summarize what he'll learn that is not here? Thanks.
Regards,

Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
Ted is available for instant help
or longer-term assistance.
Q. Is there any change in torque readings when you use a crows foot with a torque screwdriver? There is no lever arm since you are twisting the driver handle. If there is a change in torque values, how do you calculate it?
Hadji Lingstudent - Newark, New Jersey
October 2, 2009
A. To answer your question, use the following formula submitted by Joe Blendford on October 3, 2008. Using a torque screwdriver will not affect anything. Torque is a measure of force and its distance from the axis of rotation. For example; 50 in.lb. is always 50 in.lb.. The length of the torque wrench handle does not matter! 1 in.*50 lb., 2 in.*25 lb., 5 in.*10 lb. -- it is all 50 in.lb at the axis of rotation. Regardless of where you hold the handle and how hard you pull, the "neck" of the torque wrench will always "break" at 50 in.lb.. When using a torque screwdriver, the torque is the radius of the handle times the perpendicular force that is applied; still 50 in.lb at the axis of rotation. The only important dimension is the distance between wrench/screwdriver rotating axis and the fastener rotating axis on the crowsfoot.
Wrench Torque = Required Torque / (1 + Extension Length)
Where Extension Length is the distance between wrench drive rotating axis to the fastener rotating axis on the crowsfoot.
Also, this does not seem to be a practical question. For every complete rotation of the screwdriver, the crows foot will also make a complete rotation around the bolt. It would be quite tricky to turn the screwdriver as it simultaneously revolves around the bolt. If you have room to do this, then you probably don't even need to use a crows foot.
Grand Rapids, Michigan
A. An easy way to figure it out is to use known values and apply the results. torque a bolt and then torque it again with whatever wrench adapter you need to use. If it's different figure it out, if it isn't "don't fix it".
Great thread, you guys are something else. You even make it easy enough for a guy like me to understand, thanks!
- Weston, Ohio
A. It looks like your question has been answered as to the formula. However, here is a link to a calculator that will calculate the torque value for you at any angle.
www.CNCexpo.com/TorqueAdapter.aspx
- Seattle, Washington
Q. Does anyone know the effect of crows foot on torque settings?
Jared vannworkin on my boat - daytona beach Florida
February 16, 2010
Ed. note: I'll bet your teachers hated having you in their class back in school, Jared :-)
In response to Joe Blendford's and Andy Barker's suggestion to use the formula:
Wrench Torque = Required Torque / (1 + Extension Length)
Can anyone explain how this would be accurate, and why it results in a different value than the standard formula:
Wrench torque = Torque Spec * (Wrench length / Wrench + Extension Length)
I use the "standard formula" whenever necessary and believe it to be accurate. Not incorporating the wrench length into the formula dismisses the ratio of multiplication around the drive head. I can't see how this can be accurate.
- Florence, Alabama
May 9, 2010
Back to the screwdriver with a crows foot...Or in my case a torque screw driver with a 1/4" socket end attached to a crows foot. (It is a click-type set at 15 in-lbs and distance from center point of screwdriver to center point of crows foot is about 1/2")I am pretty confident that since the center points are so close, the difference in "actual" torque value versus the 15 in-lbs setting will be minimal. My only concern is the actual mechanics of turning a screw/bolt with a screwdriver that is "off center" with the crows foot attached.It seems like it would produce rotation similar to two gears turning in opposite directions. Picture the screw driver directly to the left of the screw/bolt with the crows foot engaging the left side of the fastener. If you apply a clockwise force to the driver, it seems to me that the crows foot would want to turn counter clockwise (like gears), almost "fighting" the rotation of the driver and wanting to bend in the center...Does this make sense?
Tony Stark- Beverly Hills, Florida, USA
Just to clear up and summarize everything on this thread.
Torque = Force x Perpendicular Distance.
Think about it this way. Draw a dot on a piece of paper. Now draw another dot 1" to the right of the first dot. You have now moved 1" perpendicular to the original dot (done in real life with a crows foot wrench extension) and are now able to apply torque around the first dot. You can move as far into and out of the plane of the paper as you want (done in real life with a standard wrench extension) and it will not change the torque you apply with a given force because you have moved a parallel distance. However, if you move the second dot to 2" away from the first dot (as if you put on a longer crows wrench extension) you have doubled the perpendicular distance and thus the torque has doubled, assuming the same force was applied.
Thus, the distance that matters is not from the wrench down to the bolt (aka parallel distance), but from the turning axis of the nut/bolt to the turning axis of the wrench (aka perpendicular distance). In a normal application this distance is accounted for by the calibration of the torque wrench. Thus, a 6" torque wrench and a 12" torque wrench are both putting 75 ft/lbs on a bolt when they read 75 ft/lbs, it is just a lot easier to do with the 12" because the perpendicular distance is greater. The previous post about the hypotenuse and all of that is not correct. The perpendicular distance doesn't change with an extension, and thus neither does the torque.
Here is another way to think about it. If you are trying to turn in a screw with a screw driver, does it make it easier to grab a screwdriver with a larger handle or one that is twice as long? The one with the larger handle, because you have moved your hand a perpendicular distance away from the rotation point of the screwdriver. Getting a longer screwdriver will do nothing. If you don't believe me, go out and try it.
Back to the main point. A crows foot wrench is used to attach to an extension (or directly to the wrench) to turn the rotating force 90 degrees (or parallel to the plane of the wrench handle). Thus you have essentially made the wrench longer by a percentage. In this case the formula to use is as follows:
Wrench torque = Torque Spec * (Wrench length / (Wrench length + Crows foot extension length))
* People were forgetting the parenthesis. Without them and following PEMDAS (remember that from your childhood) you will get an incorrect answer. This also lead to another confusion, which I will address below.
The reason you need wrench length is because we need to figure out by what percentage the length has changed, and thus the torque reading is effected. A 3" crows foot extension will affect the torque reading of a 6" torque wrench much more than a 12", because the percentage increase is greater. Plug in the numbers and see.
The other confusion people were having is with the equation:
Wrench Torque = Required Torque / (1 + Extension Length)
This is an INCORRECT equation that took the equation shown above and tried to reduce it algebraically. However, it was done incorrectly and does not work. This can be seen easier by the parenthesis I added. If you write out the algebra you can clearly see where the mistake was made.
Hopefully this clears things up and I will summarize by saying that the correct equation the original poster wanted, which will give you the torque applied when using a crows foot extension is as follows:
Wrench torque = Torque Spec * (Wrench length / (Wrench length + Crows foot extension length))
- Stilwell, Kansas USA
February 3, 2011
Q. I just don't see how the length of a torque wrench can have any bearing on a calculation to adjust for an extention away from the pivot point that gives additional leverage. I do see that the measured torque wrench setting will be less with an extention and have to say when I sat down and thought about it I came to
Torque(specified)= Torque(wrench)x (1+ Extension length in meters - which is the same as the simple formula you said was wrong.
My example is that I am trying to apply a torque of 50Nm to a nut but have to use a crow foot that moves the torque wrench 50mm away from the pivot. I figured that the torque wrench setting already took into account the maximum turning moment (i.e., the setting 50Nm)at the torque wrench socket, which means that it accounts for an infinite number of lengths and just means that the force applied at those lengths will vary so as to show when 50Nm is achieved at the socket.
Given the setting is in Newtons per metre, why can't I just add the additional distance from the socket to the pivot(in metres) to one metre? That way I would be applying 50N x (1m+ 0.05m) = 52.5Nm - Ops too much!
Changing the expression around
Torque(wrench)= Torque(specified)/(1+ Extension length) to give a torque wrench setting of 47.6Nm seems right.
Am I missing something or is it really that simple?
- Auckland, New Zealand
March 21, 2011
Let's draw torque wrench, 'o' is the socket and '+' is the handle:
o=====+
Let's set 5Nm on the wrench. If length of the torque wrench '====' is 0.5m, we have to put 10N force on the handle to make the wrench to click:
wrench_length * force = torque
0.5m * 10N = 5Nm
Now add a 1m length extension '-----' and don't change 5Nm setting on the torque wrench:
8-------------------o=====+
Again, when we put 10N force on the handle '+' we get 5Nm at the point 'o' and the click. Torque on the end of extension '8' now is:
(1m + 0.5m) * 10N = 15Nm.
Now check equation "Wrench Torque = Required Torque / (1 + Extension Length)":
5 = 15 ( 1 + 1) wrong.
Check equation "Wrench torque = Torque Spec * (Wrench length / (Wrench length + Crows foot extension length))":
5 = 15 ( 0.5 / (0.5 + 1)) = 15 * 0.5 / 1.5 = 15 / 1.5 * 0.5 = 10 * 0.5 = 5 ok.
There is one interesting conclusion. Common construction of torque wrench is:
8 o======+-----x
where '8' is socket and '+-----x' is handle. The actual torque when wrench clicks depends on which place of handle we are pressing at. When we are pressing near '+' the actual torque is less than if we would press near the end 'x' of the handle.
- Klaipeda, Lithuania
Just move the fist where you hold the Torque Wrench by the same amount.
Salim
- Austin, Texas, USA
Another question: If using a 6" crowfoot with a torque wrench, is the applied torque the same if the torque wrench is straight in-line with the crowfoot versus the torque wrench(not the crowfoot portion) angled at 30 degrees?
Michael Shevela- Warren, Michigan, USA
December 6, 2011
Q. I fully understand the extended torque calculation. I use it very frequently in the Aviation Industry. I recently had a discussion about adding a cheater bar to the handle of the torque wrench. I believe the extended torque calculation still holds true and that adding a ten inch extension to the handle is the equivalent to adding it to the square drive. Because ultimately you are changing the LEVER length. Can anyone clarify?
Robert Di Cenzi- Kempner, Texas, USA
December 28, 2011
A. Hi, Robert.
For children to ride on a see-saw properly requires that they exert approximately the same amount of torque around the fulcrum. The heavier kid has to lean forward or move forward and the lighter kid has to lean back or move back. That's because torque equals pull force (or push force) times the perpendicular distance from the fulcrum to the point of application of the force. If a kid leans left or right it doesn't have any effect because moving left or right didn't change the perpendicular distance (they're leaning parallel to the fulcrum pipe). The reason that straight "extensions" have no effect on torque is that they are not changing the perpendicular distance from the fulcrum (the lever length) -- it's like the kid leaning left or right, parallel to the see-saw pipe. It makes no difference how far he leans, and it makes no difference how long your extensions are.
Forgetting torque wrenches for a moment, the usual reason for using a cheater bar is to allow you to apply extra torque. Just as you might use pliers to remove a stubborn bottle cap, a cheater bar gives you more distance from the fulcrum so can apply more torque to break loose a stubborn nut or pipe fitting. I'm sure you are familiar with the fact that you can accidentally strip or break a bolt with a cheater bar. If you apply 100 pounds of pull 4 foot from the square drive with a cheater bar, that's 400 foot-pounds of torque, whereas you'd have to be superman to apply 400 foot-pounds of torque with a 1-foot long wrench. A cheater bar does change the lever length.
But the spring on a torque wrench measures torque (force X distance) not force. Whether you apply 100 pounds of pull at the end of a 1-foot wrench, or 25 pounds at the end of a 4-foot cheater, you'll get a reading of 100 foot-pounds of torque on the wrench, and you'll exert 100 foot-pounds on the bolt.
Regards,

Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
Ted is available for instant help
or longer-term assistance.
A. The equation:
Wrench Torque = Required Torque / (1 + Extension Length)
*IS* CORRECT.
However, it is in *normalized* form, that is; the effective wrench length is normalized to 1 (foot, meter, etc.)
It could be rewritten as:
Wrench Torque = Required Torque * 1 / (1 + Extension Length)
which is the *same* as the traditional form with a wrench length of 1. This works because it doesn't matter if you apply 100 lbs at one foot or 50 lbs at 2 feet, or 25 lbs at 4 feet. These all work out to 100 ft-lbs. This also explains the cheater bar; it is just easier on your arm and hand. It makes no difference at the fastener.
So with a 2 inch (.1667 ft) torque adapter extension, the torque with the extension aligned at 0 degrees is just;
Required Wrench setting = Required Torque / 1.1667
So, to get 100 ft-lbs at the fastener, you need to set the wrench to ~ 86 ft-lbs. The actual physical length of the torque wrench doesn't matter.
To find the small error when we set the 2" torque adapter at 90 degrees to the wrench, we use the Pythagorean theorem: (1 ** 2) + (.1667 ** 2) = 1.0278
[(X ** 2) means "X Squared".]
and sqrt(1.0278) = 1.0138 which is the length of the hypotenuse. So our actual torque at the fastener is 1.4% high as compared to the torque wrench setting. Except for those who are extremely fastidious and want to do a little trigonometry, this error margin can be ignored. For those who can't figure out this last paragraph; just ignore it and you will be fine.
Regards,
Dennis
- Ogden, Utah, USA
Q. How does a crows foot work at all? The center of rotation of the torque arm is not aligned with the center of rotation of the bolt. It seems the wrench is trying to shear the head off the bolt. Physics anyone?
Tim Maloy- Rock Fallos, Illinois USA
June 30, 2012
A. Hi Tim.
You are correct that the center of rotation of the torque arm is not the center of rotation of the bolt, and this can throw the torque reading off by a little; but there are no additional shear forces on the bolt, because the shape of the handle doesn't matter or enter into the free body diagram. Start by sketching a wrench handle of any arbitrary shape, and having the user apply a force (Fa) to it to loosen the bolt. For the wrench to stand still, rather than accelerate off into space, requires that the external forces applied to it are equal and opposite. So the force that the operator applies is resisted by an equal and opposite resisting force applied by the bolt (Fr). So, if you look at the external forces applied to the assembly, they are only 1) the applied force (Fa) put onto the wrench by the user, and 2) the resisting force (Fr) from the bolt.
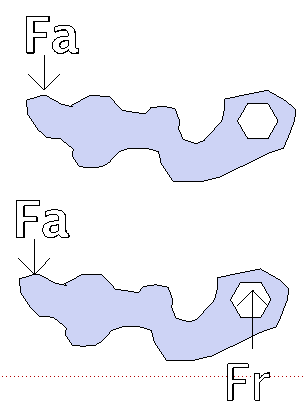
Next you can do a sum of the moments around the axis of the bolt, which must also be zero; Fa multiplied by the perpendicular distance from Fa to the axis of the bolt is the torque the user is applying to it, which is trying to accelerate the wrench in a counterclockwise direction around the axis of the bolt, and this is being resisted by the equal and opposite torque applied by the "stuckness" of the bolt, until it breaks free and the operator can push more lightly to continue the loosening.
I use the term "stuckness" because it does get a lot more complicated as we get into what is creating that "stuckness" (coefficient of friction, lead angle of the threads, and tension in the bolt), but once a bolt is beyond finger tight, what happens is that continuing to tighten it makes the far end follow the threads, which is can't do without stretching (being put into tension); and as the tension increases the threads of the bolt press harder and harder against the threads of the nut, which makes it harder and harder to continue rotating the wrench.
Regards,

Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
Ted is available for instant help
or longer-term assistance.
A. Hey everyone,
I found android apps that will do all the calculations for you. Check it out by following the link below.
https://play.google.com/store/search?q=torque+wrench&c=apps
Hope this helps everyone.
- Sterling Heights, Michigan, USA
Ed. note: The Apple apps store has similar apps for the iPhone; search for "torque wrench".
Q. Are you sure you are not confusing torque with leverage?
Torque doesn't care where you hold the handle of the torque wrench (ignoring friction), Even though the manual that came with my SK hand tools torque wrench seems to think it should. Only force on the wrench at a particular torque does. If you think there should be a torque difference between the crowfoot and what is measured at the wrench, then shouldn't the gear ratio between the two tell you what that conversion is? It looks to me like the angular movement of the wrench corresponds to the angular movement of the bolt. So shouldn't the gear ratio be 1:1? Now you've lost symmetry when using a crowfoot, but I think this is a friction issue, not an ideal case issue. What am I missing here?
-daj
- Colorado Springs, Colorado, USA
November 30, 2012
Q. In the aviation industry double offset wrenches and torque wrenches are used to tighten nuts to hold engine cylinders to the engine crankcase. The double offset wrenches used are usually 9/16" or 5/8" for general aviation engines. At the socket end the wrench bends 90 degrees runs out 2" away from the cylinder makes another 90 degree bend runs about 10" along the cylinder makes another 90 degree back toward the cylinder bend then runs 2" and terminates with a receptor for the torque wrench. Since the rotation is along the longitudinal axis of the nut being tightened I assume there is no need to adjust the recommended torque value...correct?
Bruce Epmeier- Newburgh, Indiana, USA
January 6, 2013
A. For anybody who has read through this and is still confused, Ted Mooney knows what he is talking about. His last two posts and specifically the second to last post, should help a lot of people out who seem to be getting stuck on the force applied to a torque wrench. Lots of people are confusing how a lever arm works on a torque wrench. What people are thinking is that if you increase the length of the handle and put the same amount of force on that extended length, you will get a higher torque. While this is correct logic, it is not how a torque wrench works. A torque wrench is set at a specific torque, so if you increase the length of the handle, you simply have to apply less force to make the torque wrench 'break'; you do not simply apply the same force to the handle like some people were assuming.
You can use the forces to solve for the new torque, but you have to remember that it is the force you will be applying that will change, NOT the value the torque wrench is set at.
In my situation, I have a torque wrench that is 5.75" long, and the crows foot adds 0.75", so the total lever I have on the BOLT is 6.5". My torque wrench is set to 55 in-lbs. So if I am using my torque wrench normally (with a socket, no crows foot) I have to apply 9.56 lbs at the end of the handle to reach the breaking point of the torque wrench. (F = 55in-lbs / 5.75in = 9.56 lbs).
I wanted to know how much torque I was applying to the bolt when I added the crows foot extension, so I did the following. (T = 9.56lbs * 6.5in = 62.17in-lbs) Because I am still applying 9.56 lbs at the end of the handle, and the torque wrench is still going to break at that point, the new torque is higher at 62.17 in-lbs because of the longer lever arm on the bolt.
So, to get the torque applied to the bolt back to 55 in-lbs like I wanted I can basically work backwards from that logic. If I want 55 in-lbs and my lever is 6.5 in from the torque wrench handle plus the crows foot, then the force I need to apply to the end of the handle is now 8.46 lbs (F = 55in-lbs / 6.5in = 8.46 lbs). Now, since I want to apply exactly 55 in-lbs of torque to the bolt, I need to put exactly 8.46 lbs of force on the end of the handle; so to make sure I don't put more force on the end of the handle, I need to set the torque setting on the torque wrench to break at that point. So I figure out the torque setting required on the wrench by using that force that I just found and multiplying it by the length of the torque wrench. (T = 8.46lbs * 5.75in = 48.65 in-lbs).
Therefore, I set my torque wrench to break at 48.65 in-lbs, but it is applying 55 in-lbs to the bolt, which exactly what I need.
Don't forget that your torque wrench has a percentage of error that the manufacturer should tell you, so don't expect to get the exact same result every time, but using the correct math you can find what setting you should be using.
And I'm sorry I may have rambled a bit, and not been very clear- I'm an engineer, not an English savvy person... Just draw it out and make sure to use your units in your calculations to make sure they work out properly.
**One last note, torque is easy to measure and that is why we use it for tightening specs, but in reality the CLAMPING FORCE is the spec we are actually looking for when we are figuring out how tight we want our connections. Its just that measuring the clamping force is much harder to do that measuring the torque we apply to the fastener, so be aware that you can use the same torque on two different fasteners, but if one has a less friction, you will be applying more clamping force to it and it will be tighter... Just some food for thought, and something to keep in mind if you want to get serious about tightening.
-
Ed. note: This RFQ is outdated, but technical replies are welcome, and readers are encouraged to post their own RFQs. But no public commercial suggestions please ( huh? why?).
, South Dakota, USA
July 14, 2015
A. Oops. The gear ratio model may only work in a purely rotational situation. We actually have:
-Tangential force at handle leads to torque detected at tool
-Tangential force at tool leads to torque on bolt
-For the simplified case of the crowfoot being as long as the handle, the tangential force on the tool is twice that at the handle, so the torque on the bolt should be twice that read on the tool.
-With the crowfoot, it looks like the length of the handle does matter because of this two stage tangential force-> torque conversion thing going on, which means, if you make the handle long enough, the input force location to bolt distance approaches the input force to tool hub distance, and the torque reading approaches that exerted on the bolt. It doesn't look like the length of the arm matters for normal sockets, however.
- Colorado Springs, Colorado, USA
August 20, 2016
A. Sorry I didn't read all the answers in the thread and someone may have said the same thing. Heres my answer and having a degree in mechanical engineering makes this straight forward so ill try put it in layman's terms. Having the crows foot at 90 degrees makes no difference and will still have the same negative affect as having the crows foot straight. Its understandable some people make this mistake. Whats important to understand is that torque is measure from the centre of the drive where the socket goes. Forget the length of the torque wrench it means nothing. You need to get your head around the fact that even though torque has distance in its units you can still measure torque on a single point without distance by imagining the affect it would have on said distance. For example when we talk about the torque on the end of the drive in Nm we imagine the force the drive exerts at 1 meter.
Its really easy to go off in one direction and talk endlessly about this but basically if you have a crows foot on the end of the torque wrench and you have a distance from the drive to the centre of the bolt that is 5cm. You have to add this onto you imaginary meter. You then need to adjust your units back to 1 meter by multiplying or dividing.
the aston martin workshop - London, United, Kingdom
December 28, 2016
! These formulas don't work if you change the units.
For example, a 1 foot extension bar between the nut and the head of the wrench, would require half the torque if you use ft lbs:
torque setting = Torque required / (1 + 1 ft)
but in Nm it would be
torque setting = Torque required / (1 + 0.304m)
-- which is not the same.
- Hull, England
November 11, 2019
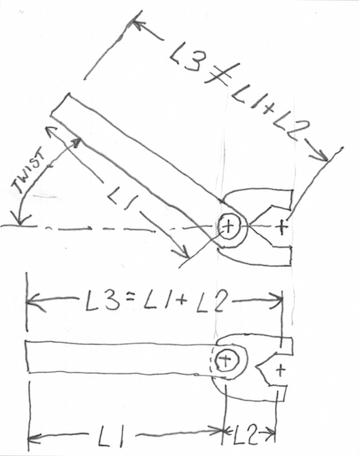
Crowfoot: A force is applied to the end of a torque wrench/crowfoot combination. We know this is not a pure torque conversion situation, since I can grab the head of the torque wrench with force f, and effect a torque on the bolt with nothing reading on the torque wrench. So we have a situation of a class II lever, where the head of the torque A. Hi David. I think the short answer is that a torque wrench cannot be meaningfully used with a crowsfoot attachment.
Regarding your analysis, please think of this: it would be correct if you were using a rigid ratchet wrench which allows no twisting at your "O" because L3, the total length of lever equals L1+L2. But as soon as the torque wrench springs allow any twisting of the handle around "O", L3 no longer equals L1+L2; this angle depends on the torque applied, the spring strength, etc.
Regards, Ted, A. Hi again. Your analysis probably remains as close as you'll get, but the idea doesn't quite work for other reasons like your statement that you can grab the head of the wrench and torque the bolt to a degree with the wrench reading zero. In fact you always inadvertently do that -- it is not possible to tighten/or loosen anything with a crows foot except by moving the head and vertical axle of your tooling arrangement in the way you would be pushing the head.
To illustrate this, I have a jet ski engine where there is a manifold over the spark plugs, with holes is the manifold centered right over the plugs to put a socket and extension through; I'm sure you've seen similar stuff. If that access hole were off center to the spark plug you would not be able to tighten the plug even with a crows foot because using the crows foot requires the head of the ratchet wrench and the extension to swing around the bolt which they would not be able to do.
You remain right that where the torque wrench is grabbed affects the torque reading when you use a crows foot but does not do so when you use a socket. Hopefully it's negligible if you hold the wrench at the end.
Regards, A. The formulas from Husky and the website of the crows foot manufacturer are approximations. R in the perpendicular crows foot orientation is still longer than just the torque wrench and in my opinion cannot be ignored ... the radius has changed, One can calculate it as the hypotenuse of a triangle with your crows foot as the short side and the original torque wrench as the other, non-hypotenuse side, but you should see that a hypotenuse now exists ....
new r = √(old torque wrench length2 + crows foot length2)
However I'm not clear on how this can be adapted to the settings on the old wrench calibrated to the old length, which is the original torque wrench handle. I would think a ratio of this effective length (hypotenuse) and the original torque wrench should be used.
|----------------------O---------------------[
^ ^
F f
|<----------L1-------->|<--------L2--------->
wrench is acting as the load, and it senses a "torque" with its gauge along the way.
t= "torque" read by the instrument =F(L1)
F=t/L1
T= F (L1+L2) = Torque on the bolt in the crowfoot
T= (t/L1)(L1+L2)
T/t=(L1+L2)/L1
So as L2 approaches 0, the reading approaches correct as L1 approaches 0, the right side blows up, since we approach the case where the technician is yanking directly on the torque wrench head with no reading, but torque to the bolt
It looks like where the technician grabs the handle does matter, and if the handle is long enough, the instrument won't care about a short crowfoot. Experimental confirmation pending...
- Colorado Springs, Colorado, USA
March 8, 2019

Ted Mooney, P.E. RET
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
Ted is available for instant help
or longer-term assistance.
November 2019
If you are talking about the small amount of give in the tool when the torque is reached, the effect is negligible with all of the torque wrenches I have used. If you are talking about putting on the crowsfoot crooked, you can still do the calculation of two virtual lengths, but there is more geometry involved.
The most common use I have for crowsfoots is for torquing fasteners not accessible with a socket.
- Colorado Springs, Colorado, USA

Ted Mooney, P.E. RET
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
Ted is available for instant help
or longer-term assistance.
- Chicago Illinois
January 22, 2021
Q, A, or Comment on THIS thread -or-
Start a NEW Thread